| ในขณะที่สัมประสิทธิ์สหสัมพันธ์ที่ใช้วัดระดับความสัมพันธ์ระหว่างตัวแ
ปรมีค่าไม่ขึ้นกับการกำหนดว่าตัวแปรใดเป็น x และตัวแปรใดเป็น y กล่าวคือ ค่าสัมประสิทธิ์สหสัมพันธ์ระหว่าง x และ y จะเท่ากับค่าสัมประสิทธิ์สหสัมพันธ์ระหว่าง y และ x แต่ในเรื่องการถดถอยจะมีการแยกตัวแปรเป็นตัวแปรอิสระ x และตัวแปรตาม y ทั้งนี้ในบางเรื่องจะมีความชัดเจนว่าตัวแปรใดเป็นตัวแปรตาม และตัวแปรใดเป็นตัวแปรอิสระ เช่น ค่าบำรุงรักษารถยนต์แปรตามอายุการใช้งานของรถ แต่อายุการใช้งานไม่แปรตามค่าบำรุงรักษา เป็นต้น แต่ก็มีบางเรื่องที่ตัวแปรสองตัวสลับบทบาทการเป็นตัวแปรตามและตัวแปรอิสระได้ เช่น อายุของสามีและอายุของภรรยา อย่างไรก็ตาม การกำหนดตัวแปร x หรือ y สลับกัน ทำให้สมการถดถอยต่างไป สมการถดถอยที่มี y เป็นตัวแปรตามใช้คาดคะเนค่า y เมื่อกำหนดค่า x แต่จะใช้สมการเดียวกันนี้คาดคะเนค่า x เมื่อกำหนดค่า y ไม่ได้ จำเป็นต้องสร้างสมการคาดคะเนขึ้นใหม่
|
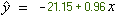
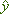 เป็น
เป็น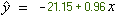
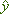 เป็น
เป็น