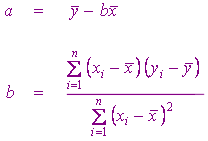| แน่นอนว่าโดยปกติเส้นถดถอยไม่สามารถจะลากผ่านค่าข้อมูลทุกค่าในแผนภาพการกระจาย นั่นคือ สมการถดถอยไม่สามารถใช้คาดคะเนค่าตัวแปรตาม y ทุกค่าได้ถูกต้องจากค่าตัวแปรอิสระ x อย่างไรก็ตาม เราต้องการสมการถดถอย หรือค่า a และ b ที่ทำให้คาดคะเนค่าตัวแปรตามได้ดีที่สุดหรือผิดพลาดน้อยที่สุด
การประมาณค่า a และ b จากข้อมูล (x1 , y1) , (x2 , y2) ,
, (xn , yn) เพื่อให้ได้เส้นตรงที่เข้ากับข้อมูลได้ดีที่สุด มีวิธีการที่เป็นที่นิยมใช้คือ วิธีกำลังสองน้อยที่สุด (least squares method) วิธีนี้จะให้ค่าประมาณ a และ b ที่ทำให้ความแตกต่างของค่าตัวแปรตามกับค่าที่คาดคะเนได้จากสมการถดถอยมีค่าน้อยที่สุด ดังนั้น ถ้าใช้สัญลักษณ์ 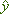 (อ่านว่า y hat) แทนค่าคาดคะเนของตัวแปรตาม สมการถดถอยที่จะประมาณขึ้นคือ (อ่านว่า y hat) แทนค่าคาดคะเนของตัวแปรตาม สมการถดถอยที่จะประมาณขึ้นคือ

และต้องการให้ค่า y ต่างจาก 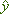 น้อยที่สุดที่ทุกจุดของค่าข้อมูล ในภาพ 2 แสดงให้เห็นแผนภาพการกระจายและเส้นถดถอยที่ดี และเส้นที่ไม่ดี พร้อมทั้งความแตกต่างของค่า y และค่า น้อยที่สุดที่ทุกจุดของค่าข้อมูล ในภาพ 2 แสดงให้เห็นแผนภาพการกระจายและเส้นถดถอยที่ดี และเส้นที่ไม่ดี พร้อมทั้งความแตกต่างของค่า y และค่า 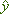 ที่จุดต่าง ๆ ที่จุดต่าง ๆ
 ภาพ 2. แผนภาพการกระจายของจุดรอบเส้นถดถอย
ภาพ 2. แผนภาพการกระจายของจุดรอบเส้นถดถอย
ค่า intercept และความชันของเส้นถดถอยที่ประมาณด้วยวิธีกำลังสองน้อยที่สุด มีสูตรดังนี้
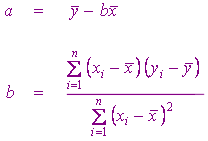
และสมการถดถอยที่ |
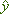 (อ่าน
(อ่าน
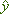 น้อย
น้อย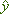 ที่
ที่
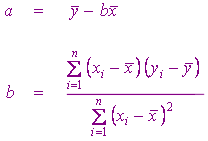
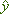 (อ่าน
(อ่าน
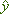 น้อย
น้อย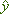 ที่
ที่