ความสัมพันธ์ในข้อมูลสองตัวแปร

สัมประสิทธิ์สหสัมพันธ์ - ค่าสัมประสิทธิ์สหสัมพันธ์

สัมประสิทธิ์สหสัมพันธ์เป็นตัววัดความสัมพันธ์ระหว่างตัวแปรในเชิงเส้นตรง ค่าของสัมประสิทธิ์สหสัมพันธ์บอกถึงระดับความสัมพันธ์ว่ามากหรือน้อย ซึ่งคือการเกาะกลุ่มของจุดรอบ ๆ แนวเส้นตรงว่าใกล้ชิดหรือกระจายห่างจากเส้น เช่น

1. ค่าสัมประสิทธิ์สหสัมพันธ์เป็น 0 จุดกระจัดกระจาย ไม่เกาะกลุ่มรอบเส้นตรง แม้ทราบค่า x ก็ไม่ช่วยให้ทราบเกี่ยวกับค่า y ดีขึ้น เพราะตัวแปรไม่เกี่ยวข้องกันในรูปแบบเส้นตรง

2. ค่าสัมประสิทธิ์สหสัมพันธ์ประมาณ 0.3 จุดเกาะกลุ่ม เริ่มเห็นรูปแบบของเส้นตรงบ้างเล็กน้อย ตัวแปรมีความสัมพันธ์กันอย่างอ่อน ๆ
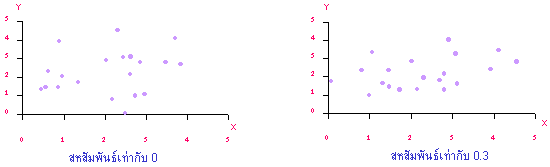
ภาพที่ 4. แสดงการกระจายของข้อมูล 4 ชุดที่มีค่ากลางและการกระจายเหมือนกัน แต่ระดับความสัมพันธ์ต่างกัน

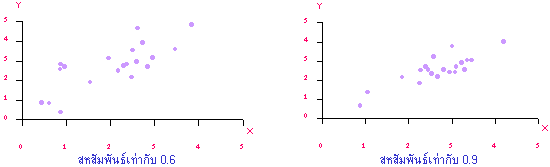
3. ค่าสัมประสิทธิ์สหสัมพันธ์ประมาณ 0.6 มองเห็นรูปแบบเส้นตรงชัดขึ้น ตัวแปร x และ y มีความเกี่ยวข้องกันมากขึ้น

4. ค่าสัมประสิทธิ์สหสัมพันธ์ใกล้ 1 จุดเกาะกลุ่มกันแนบแน่นขึ้นมากในแนวเส้นตรง ยิ่งค่าใกล้ 1 มากขึ้นเท่าใดความสัมพันธ์ในเชิงเส้นตรงระหว่างตัวแปรก็ยิ่งมากขึ้น
สหสัมพันธ์มีค่าไม่เกิน 1 ค่าสหสัมพันธ์ที่เท่ากับ 1 เรียกว่า สหสัมพันธ์อย่างสมบูรณ์ โดยจุดทั้งหมดจะตกบนแนวเส้นตรงพอดี ตัวแปรจึงมีความสัมพันธ์ในเชิงเส้นตรงอย่างแท้จริง นั่นคือ ถ้าทราบค่าตัวแปรตัวใดตัวหนึ่ง ก็จะสามารถทำนายค่าตัวแปรอีกตัวได้อย่างถูกต้อง
ค่าสัมประสิทธิ์สหสัมพันธ์ที่กล่าวมาเป็นค่าที่บอกระดับความสัมพันธ์ในทางบวก เมื่อค่า x เพิ่มขึ้น y จะเพิ่มขึ้น และเมื่อค่า x ลดลง y จะลดลง แต่ในบางครั้งตัวแปรอาจเกี่ยวข้องกันในทางลบก็ได้ กล่าวคือ เมื่อค่า x เพิ่มขึ้น y จะลดลง และเมื่อค่า x ลดลง y จะเพิ่มขึ้น เช่น รถยนต์ที่มีขนาดเครื่องยนต์มากจะกินน้ำมันมาก ดังนั้นระยะทางที่รถวิ่งได้ต่อน้ำมัน 1 ลิตรมีความสัมพันธ์ทางลบกับขนาดเครื่องยนต์

ความสัมพันธ์ในทางลบจะใช้ค่าสัมประสิทธิ์สหสัมพันธ์ที่เป็นลบ ค่าสัมประสิทธิ์สหสัมพันธ์ที่ใกล้ -1 จุดจะเกาะกลุ่มแน่นเป็นแนวเส้นตรงในแผนภาพการกระจาย โดยเส้นตรงนั้นเป็นเส้นที่ลาดลงจากมุมบนซ้ายไปยังมุมล่างขวา นั่นคือ ถ้าเส้นตรงชันสูงขึ้นค่าสัมประสิทธิ์สหสัมพันธ์จะเป็นบวก และถ้าเส้นตรงลาดลงค่าสัมประสิทธิ์สหสัมพันธ์จะเป็นลบ หากจุดทุกจุดตกบนเส้นตรงที่ลาดลง ค่าสัมประสิทธิ์สหสัมพันธ์เป็น -1 นั่นคือ ตัวแปรมีสหสัมพันธ์เป็นลบอย่างสมบูรณ์ สำหรับสหสัมพันธ์เล็กน้อยทางลบ ก็จะมีค่าสัมประสิทธ์สหสัมพันธ์ที่ใกล้ศูนย์ทางลบ เช่น -0.3


ภาพ 5. แผนภาพการกระจายของข้อมูลที่มีค่าสัมประสิทธิ์สหสัมพันธ์เป็นบวกและลบ

กล่าวโดยสรุป คือ สัมประสิทธิ์สหสัมพันธ์มีค่าอยู่ระหว่าง -1 และ 1 เสมอ เป็นค่าที่ไม่มีหน่วย ขนาดของค่าบอกถึงระดับความสัมพันธ์ว่าสูงต่ำเพียงใด โดยที่ขนาดของค่าไม่ขึ้นกับหน่วยวัดของตัวแปร

ภาพที่ 6 แสดงการแบ่งช่วงของค่าสัมประสิทธิ์สหสัมพันธ์ที่บอกความสัมพันธ์ระดับต่าง ๆ ในส่วนเครื่องหมายของค่าสัมประสิทธ์สหสัมพันธ์บอกทิศทางความสัมพันธ์ว่า สองตัวแปรมีการแปรผันค่าตามกันอย่างไร ค่าจะเป็นบวกเมื่อตัวแปรหนึ่งมีค่าเพิ่มขึ้นอีกตัวแปรก็มีค่าเพิ่มขึ้นด้วย และค่าเป็นลบเมื่อตัวแปรหนึ่งค่าเพิ่มขึ้นอีกตัวแปรค่าลดลง

ภาพ 6. ระดับความสัมพันธ์สำหรับค่าสัมประสิทธิ์สหสัมพันธ์ต่างๆ

ที่มา: เอกสารประกอบการสอน มหาวิทยาลัยเกษตรศาสตร์ 2542, วิชาบูรณาการ
หมวดการศึกษาทั่วไป รหัสวิชา 999211 คณิตศาสตร์และคอมพิวเตอร์ในชีวิตประจำวัน